|
|
|
 

|
|
| sergejzr |
|
|||
 Un salsero Профиль Группа: Админ Сообщений: 13285 Регистрация: 10.2.2004 Где: Германия г .Ганновер Репутация: 4 Всего: 360 |
Пришёл в выводы, что именно она мне нужна.
Смысл: Отрезки проецируются на кривую, а не плоскость. Смысл в том, что кучки значений надо равномерно распределить по интервалу. С помощью полученной модели затем находить положение новых точек на интервале Как проще всего реализовать такую проекцию? Поясняю в картинках Это обычная параллельная проекция С отрезка А на отрезок В  Это на кривую.  Таким образом хочу добиться, чтобы на "выпрямленной" кривой расстояния между спроецированными точками было одинакого  Это так была оттренирована система. Теперь приходит новая точка и мне надо найти её спроецированное положение вот новая тут - красная линия  Нужную кривую я создам сам (думаю колоколами интерполировать проецируемые точки). Вопрос, как легчае всего определять положение новых точек? Конечно расстояние я могу вырешать, kak sумма через (производная кривой в каждой проецируемой точки * отрезочек), Но кажется это изврат и должен быть другой, менее кривой способ добиться того, что мне надо. |
|||
|
||||
| kali |
|
|||
 Шустрый  Профиль Группа: Участник Сообщений: 139 Регистрация: 9.11.2006 Где: Минск Репутация: нет Всего: 20 |
кривая между двумя оттренированными точками будет задана функционально?
--------------------
Работая над решением задачи, всегда полезно знать ответ. |
|||
|
||||
| sergejzr |
|
|||
 Un salsero Профиль Группа: Админ Сообщений: 13285 Регистрация: 10.2.2004 Где: Германия г .Ганновер Репутация: 4 Всего: 360 |
Думаю кривую интерполировать колоколами. Это будет функция.
Чтото вроде: Сумма_по_всем_тренированным_точкам(е^(si*x^2) ) Где коефф Si надо будет подобрать. Пока ещё точно не решил, что да как, но думаю в этом направлении ждёт удача. Если возникнут другие предложения - буду рад! Добавлено через 1 минуту и 57 секунд  |
|||
|
||||
| maxim1000 |
|
|||
|
Эксперт     Профиль Группа: Участник Сообщений: 3334 Регистрация: 11.1.2003 Где: Киев Репутация: 33 Всего: 110 |
можно воспользоваться тем же подходом, который используется для выравнивания распределения генераторов случайных чисел:
берём функцию распределения: F(x)=кол-во точек < x / общее количество точек сглаживаем её как-нибудь (а то она ступенчатая будет) и для каждой точки делаем преобразование: a -> F(a) получившиеся точки будут равномерно распределены на [0,1] -------------------- qqq |
|||
|
||||
| kali |
|
|||
 Шустрый  Профиль Группа: Участник Сообщений: 139 Регистрация: 9.11.2006 Где: Минск Репутация: нет Всего: 20 |
Длина кривой F(x) на интервале от a до b равна
L=Интеграл от a до b ( Sqrt( 1+F'(x)^2 ) dx ) Если найдешь такую интерполяционную функцию, что будет аналитически считаться интеграл, то будет тебе счастье, иначе придется сумму в цикле по точкам гонять. P.S.
ИМХО утебя получается обратный эффект. Между соседними точками с малым расстоянием между собой расстояние остается небольшим, а между точками большим расстояним между собой расстояние еще больше увеличивается. Это сообщение отредактировал(а) kali - 5.6.2007, 14:54 --------------------
Работая над решением задачи, всегда полезно знать ответ. |
|||
|
||||
| sergejzr |
|
|||
 Un salsero Профиль Группа: Админ Сообщений: 13285 Регистрация: 10.2.2004 Где: Германия г .Ганновер Репутация: 4 Всего: 360 |
kali, да, всё верно, спасибо.
Короче я подумал и нашёл решение проблемы. Оно как всегда оказалось довольно простым... новая координата равна интегралу функции от начала до старой координаты. Вопрос, чему равен интеграл функции: 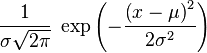 ? (Нормальное распределение ) ? (Нормальное распределение )Для этого вопроса я создал спецтему: |
|||
|
||||
| ivashkanet |
|
||||||
 Кодю потиху     Профиль Группа: Участник Клуба Сообщений: 3684 Регистрация: 23.2.2006 Где: Гомель, Беларусь Репутация: нет Всего: 149 |
sergejzr, в аналитичеких функциях этот интеграл не берется. Только приближенно. У тебя вариантов два: Либо создать таблицу значений (нужных размеров) для интеграла N(0,1), (ню = 0, сигма =1), а потом получить значение для N(m,sigma) (кста в в вики про это написано). Либо считать все самому, что менее рационально, но точнее. Добавлено @ 09:51 Не заметил, звиняюсь. Добавлено @ 09:57
Есть такое понятие как "Естественное задание прямой". Суть в том, что в качестве x используется длина кривой p (ро)от начала до этой точки.
в твоем случае можно проще:
Так вот, если ты получишь формулу своей кривой в естественных координатах, то для определения новой точки ты просто подбираешь нужное значение p, а потом вычисляешь координаты этой точки. Это сообщение отредактировал(а) ivashkanet - 4.7.2007, 10:05 |
||||||
|
|||||||
| sergejzr |
|
|||
 Un salsero Профиль Группа: Админ Сообщений: 13285 Регистрация: 10.2.2004 Где: Германия г .Ганновер Репутация: 4 Всего: 360 |
У меня получилось то что хотел (в той теме отписал немного).
Смысл в том, что регрессирую колоколами точки и в качестве новой координаты беру нормализованное значение интеграла в старой точке. Работает "на удивление" хорошо. Т.е грубо говоря использую не длину кривой (кривая - интеграл), а её градиент. где Градиент большой - разброс большой, где маленький - разброса почти нет. Сейчас в картинках отображу, вдруг кому понадобится. А ещё лучше, если кто нибудь сможет сказать, что такое уже в научной литературе есть. Тогда мне не надо будет мучатся в публикации По X - старые значения от 0 - 10, которые надо "растянуть" на интервал респектируя ожидание новых точек. Y - не важен для всех графиков кроме последнего. Собственно алгоритм 1) Берём тренировочные точки и каждой присваиваем колокол  2) Суммарно колокола дадут нам функцию распределения (чем больше плотность - тем больше значение функции)  3) Новая функция базируется на интеграле суммарной. Идея - чем выше точка в суммарной - тем больше её интеграл и наоборот. Интеграл суммарной, в свою очередь - сумма интегралов колоколов (которые апроксимируем 1/(1+ехп(-х)) )  4) ну вот и ответ  Как видим, чем больше градиент- тем больше разброс. В принципе - элементарно Т.е чем ближе изначальные точки друг к другу - тем выше значение суммарной функции - тем больше интеграл - тем "круче" градиент суммарного интеграла - тем дальше полученные точки друг от друга. Осталось доказать, что разброс действительно равномерный, но это уже дело техники |
|||
|
||||
| maxim1000 |
|
|||
|
Эксперт     Профиль Группа: Участник Сообщений: 3334 Регистрация: 11.1.2003 Где: Киев Репутация: 33 Всего: 110 |
собственно это можно описать так:
только здесь ещё использование "колоколов" привело к некоторому сглаживанию функции распределения, возможно, нелишнему... -------------------- qqq |
|||
|
||||
| sergejzr |
|
|||
 Un salsero Профиль Группа: Админ Сообщений: 13285 Регистрация: 10.2.2004 Где: Германия г .Ганновер Репутация: 4 Всего: 360 |
maxim1000, возможно я твой ответ неправильно понял
По идее выравниватель генератора должен как раз наоборот работать - увеличивать вероятность попадания новых точек на те места, где старых не было. |
|||
|
||||
| maxim1000 |
|
|||
|
Эксперт     Профиль Группа: Участник Сообщений: 3334 Регистрация: 11.1.2003 Где: Киев Репутация: 33 Всего: 110 |
нет, тогда бы распределение зависело от того, какие значения выпадали раньше
возможно, где-то и нужно подобное, но в значительно большем количестве случаев люди хотят независимые значения на каждом шагу ну и равномерно распределённые, хотя это уже не везде... -------------------- qqq |
|||
|
||||
| sergejzr |
|
|||
 Un salsero Профиль Группа: Админ Сообщений: 13285 Регистрация: 10.2.2004 Где: Германия г .Ганновер Репутация: 4 Всего: 360 |
Где можно про это почитать? Куда ссылаться? |
|||
|
||||
| maxim1000 |
|
|||
|
Эксперт     Профиль Группа: Участник Сообщений: 3334 Регистрация: 11.1.2003 Где: Киев Репутация: 33 Всего: 110 |
да, честно говоря, даже и не помню, откуда узнал
свойство простое: если x - случайная величина, F - её функция распределения, то F(x) - величина, равномерно распределённая на [0,1] (ну с некоторыми допущениями) -------------------- qqq |
|||
|
||||



















 

|
| Правила форума "Алгоритмы" | |
|
|
Форум "Алгоритмы" предназначен для обсуждения вопросов, связанных только с алгоритмами и структурами данных, без привязки к конкретному языку программирования и/или программному продукту.
Если Вам понравилась атмосфера форума, заходите к нам чаще! С уважением, maxim1000. |
| 0 Пользователей читают эту тему (0 Гостей и 0 Скрытых Пользователей) | |
| 0 Пользователей: | |
| « Предыдущая тема | Алгоритмы | Следующая тема » |
[ Время генерации скрипта: 0.0896 ] [ Использовано запросов: 21 ] [ GZIP включён ]
Реклама на сайте Информационное спонсорство
|
|
По вопросам размещения рекламы пишите на vladimir(sobaka)vingrad.ru
Отказ от ответственности Powered by Invision Power Board(R) 1.3 © 2003 IPS, Inc. |