Модераторы: Poseidon

Поиск:

Ответ в темуСоздание новой темы Создание опроса
> [Мат. анализ]Интеграл функции, Нормального распределения Гаусса 
:(
    Опции темы
sergejzr
Дата 2.7.2007, 09:17 (ссылка) | (нет голосов) Загрузка ... Загрузка ... Быстрая цитата Цитата


Un salsero
Group Icon


Профиль
Группа: Админ
Сообщений: 13285
Регистрация: 10.2.2004
Где: Германия г .Ганновер

Репутация: 11
Всего: 360
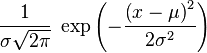Собственно вопрос, чему равен интеграл этой функции: user posted image ?
Может у кого в справочнике он завалялся smile


--------------------
Me.
FB.
LinkedIn.
ORCID.
YT.
PM WWW IM ICQ Skype GTalk Jabber AOL YIM MSN   Вверх
maxim1000
Дата 2.7.2007, 09:50 (ссылка) | (нет голосов) Загрузка ... Загрузка ... Быстрая цитата Цитата


Эксперт
****


Профиль
Группа: Участник
Сообщений: 3334
Регистрация: 11.1.2003
Где: Киев

Репутация: 24
Всего: 110
это зависит от пределов интегрирования
в общем случае, формулой не выражается, берут из таблиц или численно
однако, для случаев типа [0,+бесконечность] и вытекающих - берётся
для [-беск., +беск.] - 1 (тут даже специально нормирующий множитель есть)

Это сообщение отредактировал(а) maxim1000 - 2.7.2007, 09:50


--------------------
qqq
PM WWW   Вверх
sergejzr
Дата 2.7.2007, 11:52 (ссылка) | (нет голосов) Загрузка ... Загрузка ... Быстрая цитата Цитата


Un salsero
Group Icon


Профиль
Группа: Админ
Сообщений: 13285
Регистрация: 10.2.2004
Где: Германия г .Ганновер

Репутация: 11
Всего: 360
Мдя... тоже на это наткнулся... мне как раз надо для любых границ. Хотя мне именно гаусса в принципе не обязательно....
Другой вариант, интеграл колокола должен получится чем-то вроде жирной линии:
user posted image
Что это за функция? Я её смогу для своих нужд заюзать

Поясню... задача инженерная, поэтому точность здесь относительно не важна. Важна модель.


ПС:
maxim1000, спасибо за перенос в центр smile в попыхах не подумал...


--------------------
Me.
FB.
LinkedIn.
ORCID.
YT.
PM WWW IM ICQ Skype GTalk Jabber AOL YIM MSN   Вверх
maxim1000
Дата 2.7.2007, 12:31 (ссылка) | (нет голосов) Загрузка ... Загрузка ... Быстрая цитата Цитата


Эксперт
****


Профиль
Группа: Участник
Сообщений: 3334
Регистрация: 11.1.2003
Где: Киев

Репутация: 24
Всего: 110
можно его численно посчитать
во многих математических библиотеках, по идее, должно быть


--------------------
qqq
PM WWW   Вверх
sergejzr
Дата 2.7.2007, 12:47 (ссылка) | (нет голосов) Загрузка ... Загрузка ... Быстрая цитата Цитата


Un salsero
Group Icon


Профиль
Группа: Админ
Сообщений: 13285
Регистрация: 10.2.2004
Где: Германия г .Ганновер

Репутация: 11
Всего: 360
Численный возьму только если всё остальное не поможет. Он попросту неинтересен, хотя и сработает конечно.
S- образная функция мне даже наверное больше подойдёт как аппроксимация интеграла...


--------------------
Me.
FB.
LinkedIn.
ORCID.
YT.
PM WWW IM ICQ Skype GTalk Jabber AOL YIM MSN   Вверх
sergejzr
Дата 2.7.2007, 18:13 (ссылка) | (нет голосов) Загрузка ... Загрузка ... Быстрая цитата Цитата


Un salsero
Group Icon


Профиль
Группа: Админ
Сообщений: 13285
Регистрация: 10.2.2004
Где: Германия г .Ганновер

Репутация: 11
Всего: 360
что это за функция?


user posted image


--------------------
Me.
FB.
LinkedIn.
ORCID.
YT.
PM WWW IM ICQ Skype GTalk Jabber AOL YIM MSN   Вверх
Aloha
Дата 2.7.2007, 19:27 (ссылка) | (нет голосов) Загрузка ... Загрузка ... Быстрая цитата Цитата


.
**


Профиль
Группа: Участник Клуба
Сообщений: 351
Регистрация: 14.5.2006

Репутация: 97
Всего: 165
sergejzr

Вариантов много можно придумать. Например, арктангенс (с соответствующими коэффициентами):
user posted image

или гиперболический тангенс:
user posted image

Но чаще всего в качестве модели s-образной кривой используют логистические функции общего вида:
user posted image

Вот, к примеру, такая:
user posted image
PM   Вверх
cardinal
Дата 3.7.2007, 01:47 (ссылка) | (нет голосов) Загрузка ... Загрузка ... Быстрая цитата Цитата


Инженер
****


Профиль
Группа: Экс. модератор
Сообщений: 6003
Регистрация: 26.3.2002
Где: Германия

Репутация: 15
Всего: 99
Интересно зачем это нужно... smile 


--------------------
Немецкая оппозиция потребовала упростить натурализацию иммигрантов
В моем блоге: Разные истории из жизни в Германии

"Познание бесконечности требует бесконечного времени, а потому работай не работай - все едино".  А. и Б. Стругацкие
PM   Вверх
sergejzr
Дата 3.7.2007, 09:06 (ссылка) | (нет голосов) Загрузка ... Загрузка ... Быстрая цитата Цитата


Un salsero
Group Icon


Профиль
Группа: Админ
Сообщений: 13285
Регистрация: 10.2.2004
Где: Германия г .Ганновер

Репутация: 11
Всего: 360
Aloha, спасибо большое! smile
Цитата(cardinal @  3.7.2007,  00:47 Найти цитируемый пост)
Интересно зачем это нужно...

http://forum.vingrad.ru/forum/topic-149114.html
http://forum.vingrad.ru/forum/topic-154905.html



--------------------
Me.
FB.
LinkedIn.
ORCID.
YT.
PM WWW IM ICQ Skype GTalk Jabber AOL YIM MSN   Вверх
cardinal
Дата 3.7.2007, 10:34 (ссылка) | (нет голосов) Загрузка ... Загрузка ... Быстрая цитата Цитата


Инженер
****


Профиль
Группа: Экс. модератор
Сообщений: 6003
Регистрация: 26.3.2002
Где: Германия

Репутация: 15
Всего: 99
Ну тогда думаю третий вариант, предложенный Aloha в самый раз...


--------------------
Немецкая оппозиция потребовала упростить натурализацию иммигрантов
В моем блоге: Разные истории из жизни в Германии

"Познание бесконечности требует бесконечного времени, а потому работай не работай - все едино".  А. и Б. Стругацкие
PM   Вверх
sergejzr
Дата 3.7.2007, 10:46 (ссылка) | (нет голосов) Загрузка ... Загрузка ... Быстрая цитата Цитата


Un salsero
Group Icon


Профиль
Группа: Админ
Сообщений: 13285
Регистрация: 10.2.2004
Где: Германия г .Ганновер

Репутация: 11
Всего: 360
Ага, оно почти идеально. Посмотрим, как оно выйдет...



--------------------
Me.
FB.
LinkedIn.
ORCID.
YT.
PM WWW IM ICQ Skype GTalk Jabber AOL YIM MSN   Вверх
Elfet
  Дата 3.7.2007, 19:53 (ссылка) | (нет голосов) Загрузка ... Загрузка ... Быстрая цитата Цитата


Белый и Пушистый
****


Профиль
Группа: Awaiting Authorisation
Сообщений: 3776
Регистрация: 2.4.2003

Репутация: нет
Всего: 16
А вот что мне Mathematica выдала:
user posted image
user posted image


--------------------
PHP Чат Скрипт
PM MAIL WWW Skype   Вверх
cardinal
Дата 3.7.2007, 20:19 (ссылка) | (нет голосов) Загрузка ... Загрузка ... Быстрая цитата Цитата


Инженер
****


Профиль
Группа: Экс. модератор
Сообщений: 6003
Регистрация: 26.3.2002
Где: Германия

Репутация: 15
Всего: 99
То есть в точности ничего полезного smile 


--------------------
Немецкая оппозиция потребовала упростить натурализацию иммигрантов
В моем блоге: Разные истории из жизни в Германии

"Познание бесконечности требует бесконечного времени, а потому работай не работай - все едино".  А. и Б. Стругацкие
PM   Вверх
sergejzr
Дата 3.7.2007, 21:57 (ссылка) | (нет голосов) Загрузка ... Загрузка ... Быстрая цитата Цитата


Un salsero
Group Icon


Профиль
Группа: Админ
Сообщений: 13285
Регистрация: 10.2.2004
Где: Германия г .Ганновер

Репутация: 11
Всего: 360
erf это как раз 1/ехп(-х) (в умных книжках посмотрел smile )

Кстати в общем задумка работает довольно неплохо. Правда аппроксимация даёт нехилую погрешность, но для проверки модели подошла.


--------------------
Me.
FB.
LinkedIn.
ORCID.
YT.
PM WWW IM ICQ Skype GTalk Jabber AOL YIM MSN   Вверх
maxim1000
Дата 3.7.2007, 22:43 (ссылка) | (нет голосов) Загрузка ... Загрузка ... Быстрая цитата Цитата


Эксперт
****


Профиль
Группа: Участник
Сообщений: 3334
Регистрация: 11.1.2003
Где: Киев

Репутация: 24
Всего: 110
Цитата(sergejzr @  3.7.2007,  21:57 Найти цитируемый пост)
1/ехп(-х)

хм... вряд ли...
1/exp(-x)=exp(x) smile

Добавлено через 1 минуту и 41 секунду
там дано определение erf(z)=I[0..z] exp(-t*t)dt *2/sqrt(pi)


--------------------
qqq
PM WWW   Вверх
Ответ в темуСоздание новой темы Создание опроса
Правила форума "Центр помощи"

ВНИМАНИЕ! Прежде чем создавать темы, или писать сообщения в данный раздел, ознакомьтесь, пожалуйста, с Правилами форума и конкретно этого раздела.
Несоблюдение правил может повлечь за собой самые строгие меры от закрытия/удаления темы до бана пользователя!


  • Название темы должно отражать её суть! (Не следует добавлять туда слова "помогите", "срочно" и т.п.)
  • При создании темы, первым делом в квадратных скобках укажите область, из которой исходит вопрос (язык, дисциплина, диплом). Пример: [C++].
  • В названии темы не нужно указывать происхождение задачи (например "школьная задача", "задача из учебника" и т.п.), не нужно указывать ее сложность ("простая задача", "легкий вопрос" и т.п.). Все это можно писать в тексте самой задачи.
  • Если Вы ошиблись при вводе названия темы, отправьте письмо любому из модераторов раздела (через личные сообщения или report).
  • Для подсветки кода пользуйтесь тегами [code][/code] (выделяйте код и нажимаете на кнопку "Код"). Не забывайте выбирать при этом соответствующий язык.
  • Помните: один топик - один вопрос!
  • В данном разделе запрещено поднимать темы, т.е. при отсутствии ответов на Ваш вопрос добавлять новые ответы к теме, тем самым поднимая тему на верх списка.
  • Если вы хотите, чтобы вашу проблему решили при помощи определенного алгоритма, то не забудьте описать его!
  • Если вопрос решён, то воспользуйтесь ссылкой "Пометить как решённый", которая находится под кнопками создания темы или специальным флажком при ответе.

Более подробно с правилами данного раздела Вы можете ознакомится в этой теме.

Если Вам помогли и атмосфера форума Вам понравилась, то заходите к нам чаще! С уважением, Poseidon, Rodman
 
0 Пользователей читают эту тему (0 Гостей и 0 Скрытых Пользователей)
0 Пользователей:
« Предыдущая тема | Центр помощи | Следующая тема »

Подписаться на тему | Подписка на этот форум | Скачать/Распечатать тему


 




[ Время генерации скрипта: 0.1127 ]   [ Использовано запросов: 22 ]   [ GZIP включён ]


Реклама на сайте     Информационное спонсорство

 
 По вопросам размещения рекламы пишите на vladimir(sobaka)vingrad.ru
Отказ от ответственности     Powered by Invision Power Board(R) 1.3 © 2003  IPS, Inc.